How to Calculate the Present Value of Future Lease Payments
Executive Summary
- All leases including operating leases must now be present valued and will be recognized on the balance sheet
- The standards setters do not implicitly state a specific formula to apply when calculating the present value of future lease payments
- There are three present functions available in Excel:
- PV: present value future inflows or outflows amounts based on periods
- NPV: present values future amounts in which the NPV function automatically assumes all the time periods are equal
- XNPV: uses specific dates that correspond to each amount being discounted in the series - Other present value methods: It can get incredibly granular. The XNPV used in Excel does not adhere to the standards setters at the IASB (IFRS 16) as the day count convention (how you calculate interest based on the discount rate input) is 365/fixed as opposed to Actual/Actual
- The most accurate present value formulas/function will take into consideration the date the payments occur
How to calculate the present value
There are many ways to skin a cat. With lease accounting, how you present value your lease liability is no exception. This is a critical area of the standard and is susceptible to manual error. Not to mention the right-of-use asset is derived from the lease liability. If your lease liability present value calculation is incorrect, so is the right-of-use asset value.
The objective of this document is to:
- Clarify what "present value" means
- How to apply present value concepts in Microsoft Excel to lease accounting
- Discuss what's the best present value calculation methodology.
The topics we're about to cover are especially vital if you're going to calculate your lease liability in Microsoft Excel manually. Not to mention if you've opted with a lease accounting solution, you may want to recalculate your numbers for peace of mind.
What does the standard say?
Before going any further, what do the applicable standards state concerning how to present value a lease liability?
IFRS 16:
At the commencement date, a lessee shall measure the lease liability at the present value of the lease payments that are not paid at that date. The lease payments shall be discounted using the interest rate implicit in the lease, if that rate can be readily determined.
US GAAP ASC 842:
The lease liability is the present value of the lease payments not yet paid, discounted using the discount rate for the lease at lease commencement.
As per the above, the standards provide no more detail then the lessee must present value the lease payments.
What does present value mean?
Present value
It’s essential to understand the time value of money concept. A dollar today isn’t worth the same as a dollar tomorrow. This is at the core of IFRS 16 and ASC 842, the future lease cash outflows are present valued to represent the value of the lease liability at a particular point in time.
Common present value calculation attributes
When calculating the present value of the future lease payments regardless of the methodology, all calculations will require:
- Discount rate: the rate used that will present value the future lease payments
- Future cash flows: all calculations require a future set of cash flows (lease payments); these are the amounts that will be present valued.
Is present value the same as net present value?
Investopedia describes the difference as the following:
Present value (PV) is the current value of a future sum of money or stream of cash flow given a specified rate of return. Meanwhile, net present value (NPV) is the difference between the present value of cash inflows and the present value of cash outflows over a period of time.
The main difference between PV and NPV is the NPV formula accounts for the initial capital outlay required to fund a project, making it a net figure, while the PV calculation only accounts for cash inflows.
So the difference is how you use the formula. A net present value includes both outflows and inflows of cash, while a present value only includes inflows or outflows.
Present value formulas in Microsoft Excel:
Many mathematical formulas can be used to calculate the present value of a figure. For this article we’ll only cover those offered in excel which are:
- PV: Present Value
- NPV: Net Present Value
- XNPV: X Net Present Value
To display the impact of using each excel function, the same lease example will be used:
A lessee signs into a contract noting the following details:
- The lease commencement date is on January 1, 2020, in which the lessee pays in advance at the start of every year.
- The lease term is for 10 years
- The lease payments start at $1,000 per annum and increase 5% each year.
The lessee determines the incremental borrowing rate/discount rate of 6%
Present Value
FV / (1 + r)n
Where
- FV is the future value
- r is the required rate of return
- n is the number of periods
When you use the PV function in excel it details the arguments used in the function
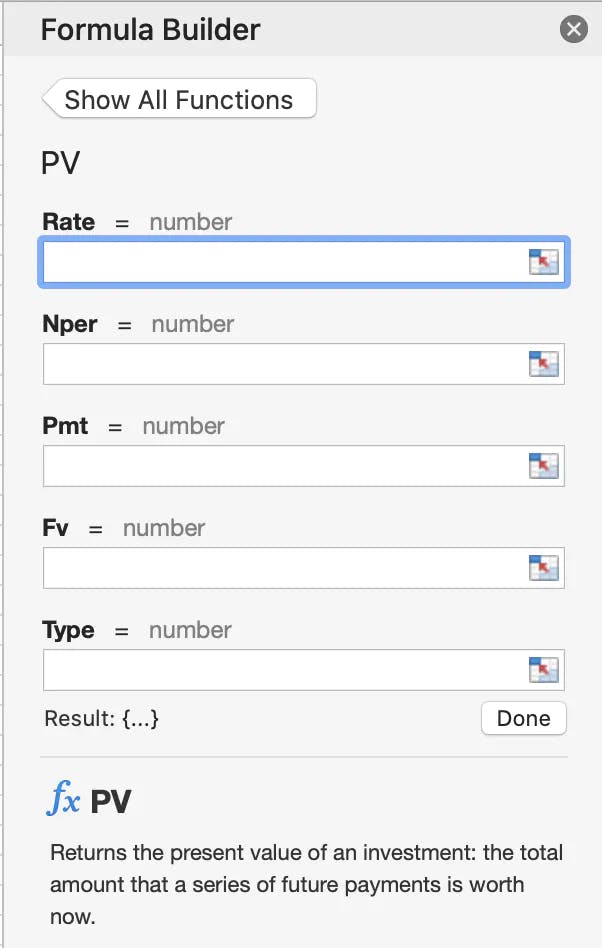
Rate: The interest rate per period. For example, if you obtain an automobile loan at a 10 percent annual interest rate and make monthly payments, your interest rate per month is 10%/12, or 0.83%. You would enter 10%/12, or 0.83%, or 0.0083, into the formula as the rate.
Nper: The total number of payment periods in an annuity. For example, if you get a four-year car loan and make monthly payments, your loan has 4*12 (or 48) periods. You would enter 48 into the formula for nper.
Pmt: The payment made each period and cannot change over the life of the annuity. Typically, pmt includes principal and interest but no other fees or taxes. For example, the monthly payments on a $10,000, four-year car loan at 12 percent are $263.33. You would enter -263.33 into the formula as the pmt. If pmt is omitted, you must include the fv argument.
FV: The future value or a cash balance you want to attain after the last payment is made. If fv is omitted, it is assumed to be 0 (the future value of a loan, for example, is 0). For example, if you want to save $50,000 to pay for a special project in 18 years, then $50,000 is the future value. You could then make a conservative guess at an interest rate and determine how much you must save each month. If fv is omitted, you must include the pmt argument.
Type: The number 0 or 1 and indicates when payments are due.
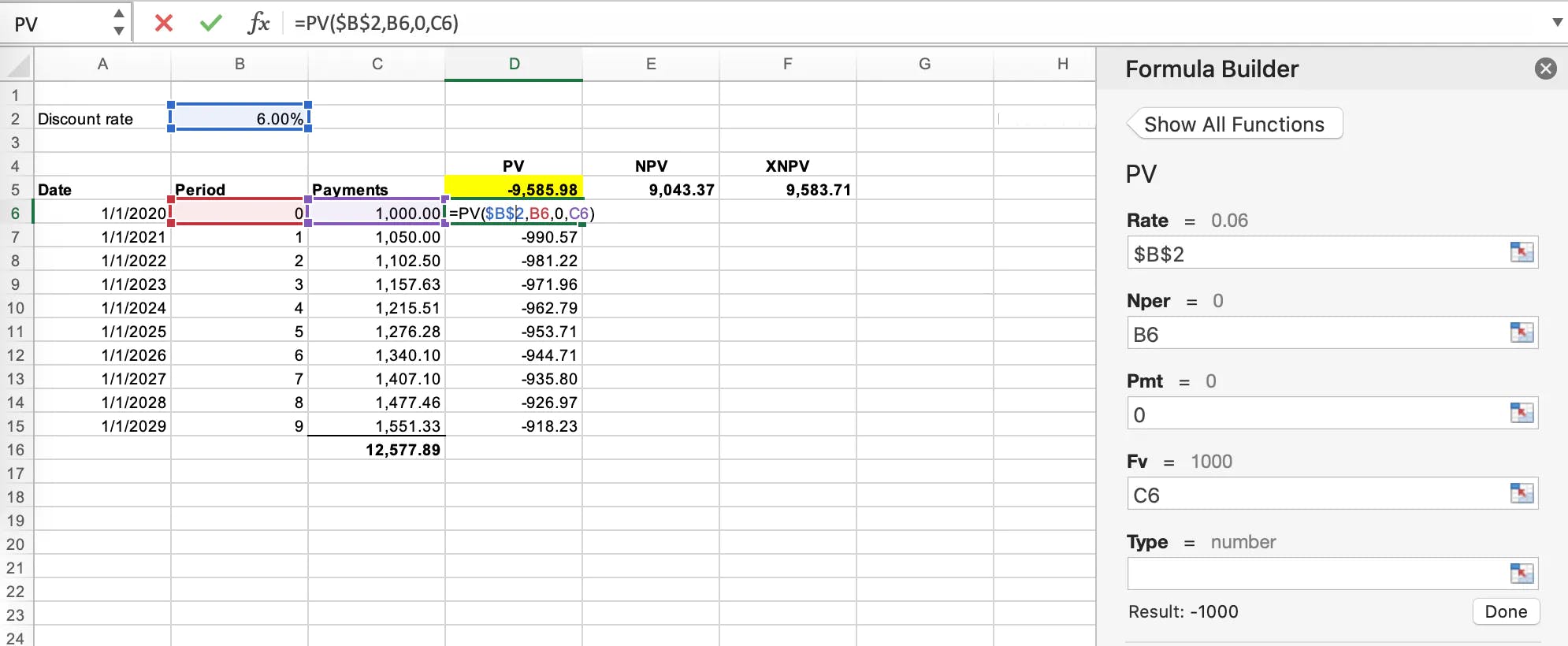
How is that number calculated?
As illustrated in the screenshot you will need to:
- Add the future cash flows due to the lessor
- Add the period the cash flows are in relation to in this case 0 to 9
- Decide on a discount rate to present value the future payments in this example 6%
Each individual period is present valued and the total sum of those figures equals $9,585.98.
The key input in this present value excel function is each payment is given a period. The first period is 0, which results in the present value amount of $1,000 given it’s not a future amount. On the other hand in period 1 the present value of 1,050 is $990.57.
This illustrates how important the period is or “Nper” is in excel, bearing in mind this is a period input as opposed to a date input.
Net Present Value
R1/ (1+i)1 + R2/(1+i)2 + R3/(1+i)3
In reference to the NPV formula above:
- R1 = Net Cash flow in period one, R2 = Net Cash flow in period two, R3= Net Cash flow in period three and i = the discount rate.
Using the same fact pattern as the example used for the PV formula in excel it looks like this:
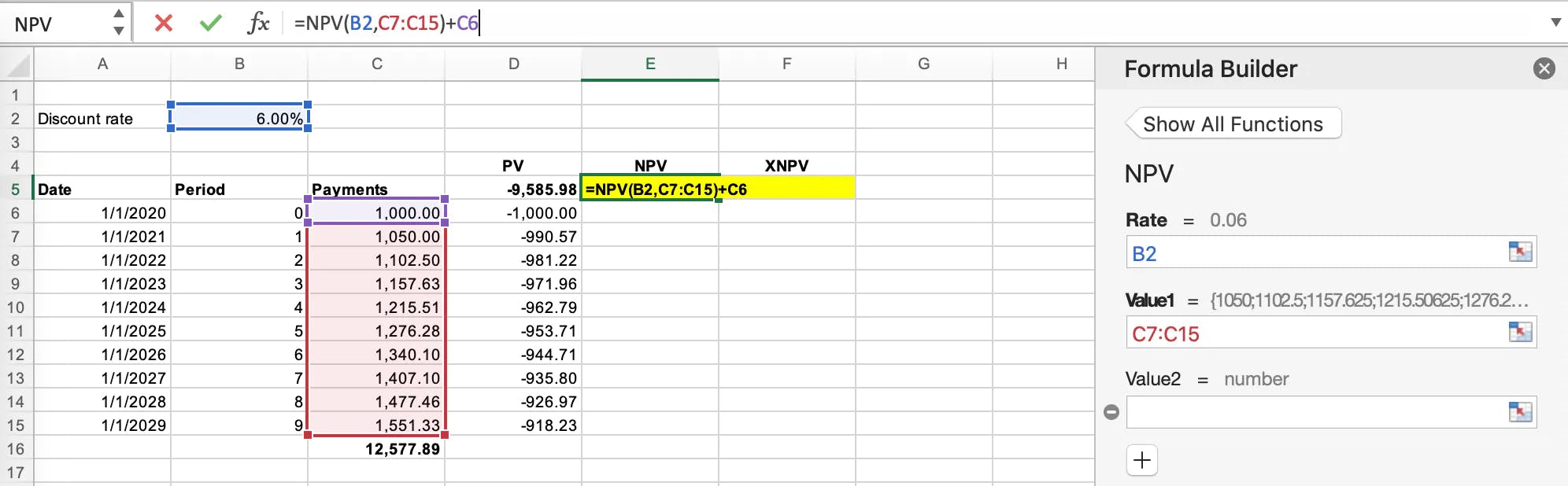
Unlike the PV function in excel, the NPV function/formula does not consider any period. The function automatically assumes all the time periods are equal.
The total if you included the $1,000 on day 1 is $9,043.37. Technically you should not present value a figure on day 0 as there’s no impact of the time value of money.
When you present value all future payments and add $1,000 to the NPV amount, the total is $9,585.98 identical to the PV formula.
XNPV
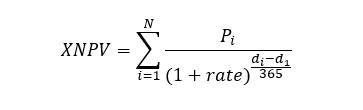
where:
- di = the ith payment date
- d1 = the 0'th payment date
- Pi = the ith payment
The last present value formula available is also the most accurate. The XNPV function requires one more input when compared to NPV being the date of the future lease payment.
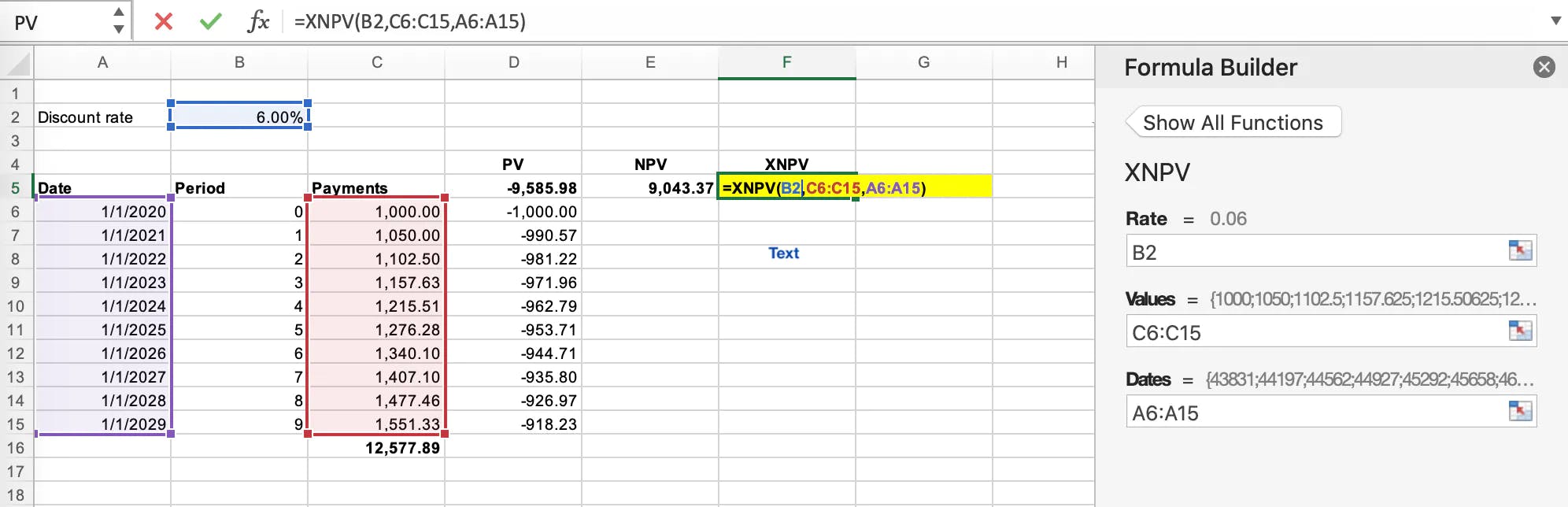
When using an XNPV function in excel, the present value of the future payments is $9,583.71 resulting in a $2.26 difference between the NPV & PV methodology when recording the lease liability on the balance sheet. In this particular example, the present value amount is relatively small. The difference between the two functions will be more significant when a more substantial sum is present valued. Regardless of this fact, from an auditor's perspective, they will not raise an audit difference based on the present value function selected.
Which methodology should I use?
Here we discuss some options that are available to you.
NPV
Positives:
- The most straightforward calculation to perform, the only inputs required are:
- Discount rate
- Future cash flows - Audit firms will likely use the same methodology
Negatives:
- The least accurate method:
- Automatically assumes all the time periods are equal
- One-off payments, modifications mid-month will not be present valued accurately
PV
Positives:
- Provides a higher level of accuracy compared to NPV
Negatives:
- Time-consuming to correctly allocate the periods, e.g. in period 11.25, there is a CPI increase. Using a date methodology is far quicker.
XNPV
Positives:
- The most accurate as it present values each payment based on the date the payment occurs.
- Incredibly flexible can be done daily calculations.
Negatives:
- It can be more time consuming compared to NPV to get the added accuracy.
- The function is not as well known as the NPV function.
Conclusion
Given the ease and that audit firms themselves use the same methodology when calculating a lease liability majority of companies will use an NPV calculation. This works for straightforward lease accounting scenarios. However, it will not be able to handle irregular payments to the same accuracy as XNPV.
Bonus section - why when I calculate the IFRS 16 Illustrative example in Microsoft Excel, using a daily XNPV function, it does not agree to the standard’s examples?
The difference is driven by the way Microsoft Excel’s XNPV calculation formula works. The XNPV function assumes interest on the lease liability is calculated based on 365 days a year as opposed to the actual days occurring in the calendar year. This calculation methodology is called actual 365/fixed. In the IFRS 16 Illustrative examples, the calculation methodology is slightly different. They use Actual/Actual ISDA, which calculates interest based on how many actual days in a year. For example, the year 2020 has 366 days. This is what is driving the difference between the Microsoft Excel numbers and that of the standard setters.

